
유클리드가 알렉산드리아에서 이집트 왕 프톨레마이오스 1세 소테르에게 그의 연구를 설명하고 있다. 이 그림은 1866년 루이 피기에가 그린 것이다.

골드바흐가 오일러에게 보낸 편지에 사소한 잡담 같은 것은 없다. 수학자들의 편지는 대부분 이렇다
"난 좀 더 재미나게 사는 모습 좀 보고 싶다... 나만의 바램인가??" 최근 어떤 지인이 한 말인데, 전 현재 없는 자들을 "참여와 공유" 정신으로 무장시키는데에 작업중...
https://blog.daum.net/samsongeko/11536
"난 좀 더 재미나게 사는 모습 좀 보고 싶다... 나만의 바램인가??" 최근 어떤 지인이 한 말인데,
전 현재 그 초단기대박계획(MOAI) 대중형 총 10기의 10230명 없는 자들을 "참여와 공유" 정신으로 무장시키고 같이 부우자가 되기를 꿈꾸는 "동학개미들의 선봉장 - 돈키호테"를 꿈꾸고 있는 중입니
blog.daum.net

전 현재 그 초단기대박계획(MOAI) 대중형 총 10기의 10230명 없는 자들을 "참여와 공유" 정신으로 무장시키고 같이 부우자가 되기를 꿈꾸는 "동학개미들의 선봉장 - 돈키호테"를 꿈꾸고 있는 중입니다~~~^^ 이보다 더 재미있게 사는 방법도 없을꺼 같은데, 증권업계의 백 종원씨가 되려고 하는데, 여전히 난관이 있고요~~~^^ 결국 법원에서 벌금형을 내려 이런 형태보다는 투자(협동)조합 방식을 내년 대중형 재도전 1기 10명때부터 적용시키는 작업을 GI 법무팀과 재협의중입니다... 이번주내내 이 일로 장고중입니다... 게코(Gekko)

(2019.4.25)NICA/GCC 바이블 - 강추, 이 단어 오랫만에 다시 써보네요.. 그 서민갑부입니다...
https://blog.daum.net/samsongeko/7995
골드바흐의 추측
1742년에 프로이센의 수학자인 크리스티안 골드바흐는 스위스의 수학자이자 물리학자인 레온하르트 오일러에게 편지를 썼다. 이 편지에서 골드바흐는 ‘2보다 큰 모든 정수는 3개 소수의 합으로 쓸 수 있다.’는 가설을 세웠다.
그는 1도 소수로 생각했지만 수학자들은 받아들이지 않았다. 이 추론은 그 이후로 다듬어져 ‘2보다 큰 모든 짝수는 두 개 소수의 합으로 쓸 수 있다.’라고 수정되었다.
골드바흐는 자신의 생각을 증명할 수는 없었다(그래서 정리(定理)가 아닌 추론(推論)이다). 그리고 지금까지 어느 누구도 이것을 증명한 적은 없다. 컴퓨터로 최고 1,018(2007년 3월)까지 모든 수를 검증했지만, 이 이론은 아직 증명되지 않았다.

소수
Prime number , 素數

소수는 특별한 정수이다. 소수는 자기 자신과 1을 제외하고는 인수가 없는(어떤 수로도 나눠지지 않는) 수이다. 20 이하의 소수는 2, 3, 5, 7, 11, 13, 17, 19(1은 보통 포함시키지 않음)이다.
수가 점점 커질수록 소수가 나타나는 횟수는 줄어들지만 소수는 신기할 정도로 계속해서 나타난다. 1,000,000 근처의 수에서도 소수는 대략 14개에 한 개꼴로 나타난다.
사람들은 수천 년 동안 소수에 대해 연구해왔고 미신적이거나 종교적인 중요성을 소수에 부여해왔다.
그리스 수학자인 유클리드는 기원전 300년경에 소수가 끊이지 않고 계속해서 나타난다는 사실을 최초로 증명했다. 하지만 2000년 이상이 지난 지금도 소수를 구하는 공식은 알려지지 않았다.
소수는 별로 특별할 게 없는 수처럼 생각되기도 하고 실질 인수가 없는 결함이 있는 수로 여겨지기도 한다. 하지만 소수를 둘러싼 흥미로운 현상들이 있어 소수는 정수론의 주요 연구 대상이 되어왔다.
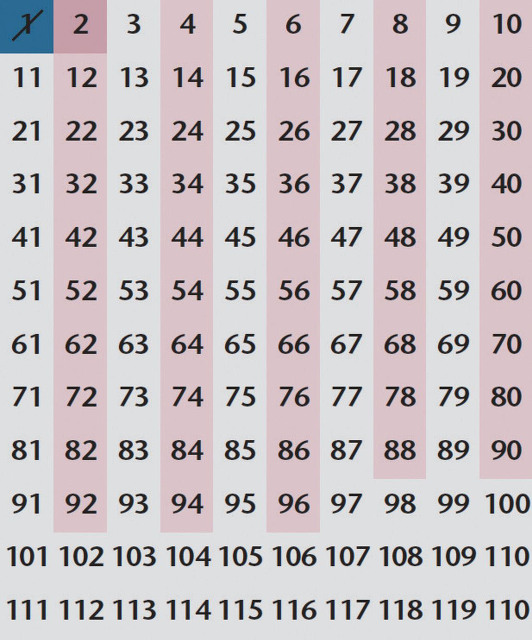
에라토스테네스의 체
고대 그리스 수학자인 에라토스테네스는 소수를 찾는 간단한 알고리즘을 개발했다. 이 알고리즘을 에라토스테네스의 체라고 한다.
에라토스테네스
에라토스테네스(276~194BC)는 리비아에서 태어났지만 이집트의 수도였던 알렉산드리아에서 활동하고 이곳에서 사망했다. 아르키메데스의 친구이기도 했던 그는 알렉산드리아의 도서관을 맡고 있었다.
기원전 250년경에 그는 혼천의를 발명했다. 혼천의는 구(球) 형태로 별의 움직임을 보여주거나 예측할 수 있는 교차하는 고리로 이루어졌다. 이것은 18세기까지 천문학 도구로 사용되었다.
에라토스테네스는 또한 경도와 위도를 측정할 수 있는 시스템을 개발했고 그때까지 알려져 있던 전 세계의 지도를 그렸다. 그는 최초로 지구의 원주를 계산해 기록해놓았다.
이후에 작가인 카이사레아의 에우세비우스는 지구에서 태양까지의 거리를 계산할 수 있었던 것이 에라토스테네스 덕분이라고 말했다. 에우세비우스가 계산한 거리는 현재 계산된 거리에서 1% 이내의 오차 범위에 있다.
소수를 걸러내는 방법
1. 정사각형의 격자 무늬를 그리고 그 안에 1부터 시작해서 소수를 찾으려는 최대 범위의 수를 모두 적는다. 1을 지운다. 1은 소수가 아니다.
2. 첫 번째 소수는 2이다. 소수 목록의 제일 위에 이 숫자를 적고, 2가 곱해진 모든 수를 지운다.
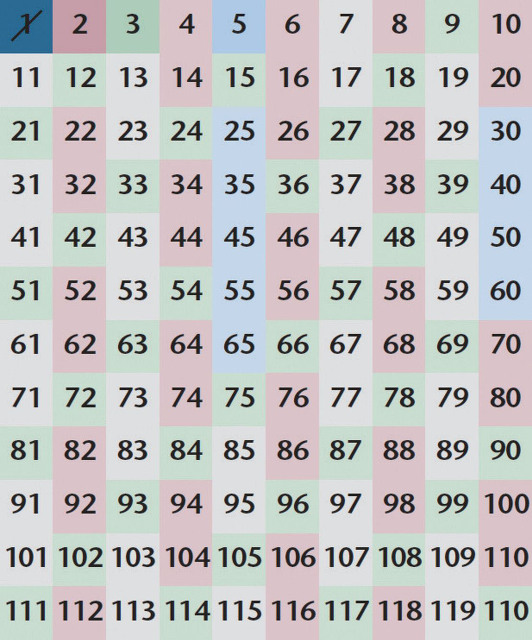
3. 그 다음 남아 있는 수가 다음 소수인 3이다. 그러므로 이 숫자를 소수 목록에 적고, 3이 곱해진 모든 수를 지운다.
4. 그 다음에 남아 있는 수는 그 다음 소수인 5이다. 이 수를 소수 목록에 적고 5가 곱해진 모든 수를 지운다.

5. 사각 격자 안의 마지막까지 이 과정을 반복한다. 목록에 있는 (사각 격자 안에서 지워지지 않은) 숫자가 소수이다.
소수 찾기
작은 수의 소수는 찾기 쉽다. 이 수는 머릿속으로 계산해도 찾을 수 있다. 하지만 큰 수의 소수는 점점 찾기 어려워진다. 소수 이론에서는 소수가 나타나는 빈도를 예측하고자 한다.
프랑스 수학자인 앙드리앵 마리 르장드르가 1978년에 x 이하의 소수 개수는 대략적으로 다음과 같다는 것을 보여주었다.
x/ln(x)
여기에서 ln(x)는 자연 로그 x이다. x의 크기가 커지면 근사치의 부정확성은 줄어든다. x가 소수가 될 수 있는 확률은 1/ln(x)이다. 예를 들어, 1,000,000의 자연 로그는 13.8이므로 1,000,000 근처의 숫자가 소수가 될 가능성은 1/13.8이다.
쌍둥이 소수
쌍둥이 소수는 2만큼씩 차이가 나는 쌍으로 이루어진 소수들이다. 쉽게 알 수 있는 예는 3과 5, 5와 7, 11과 13, 17과 19 등이다. 쌍둥이 소수 추론에 따르면 쌍둥이 소수는 무한개이다.
어떤 시점에 쌍둥이 소수가 존재하기만 하면 되기 때문에 이 말은 일리가 있다. 하지만 이것이 사실인지는 증명되지 않았다. 또한 증명된 적이 있는 ‘약한’ 쌍둥이 소수 추론도 있다.
이 추론에서는 x 이하의 숫자에서 쌍둥이 소수의 개수는 매우 복잡한 다음 공식으로 대략 구할 수 있다.
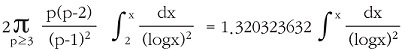
이 공식을 이해하는 것이 중요한 것은 아니다. 생각해볼 만한 것은 ‘왜 이런 공식이 존재하는 것일까?’ 하는 것이다. 숫자가 과연 무엇이길래 이러한 공식을 만들 수 있을까? 이 공식 중간에 있는 숫자는 소수의 상수라고 불리는 1.320323632이다.
이 상수는 쌍둥이 소수를 예측하는 것 말고는 다른 수와 별 상관이 없다.

향년 54세로 돌아가신 어머니 병중 2000년5월에 출간된 책입니다...

아포스톨로스 독시아디스
1953년 호주의 브리스배인 출생으로 그리스의 아덴에서 자랐다.
어려서부터 수학에 대한 남다른 재능을 보여 15살이라는 어린 나이로 뉴욕의 콜럼비아 대학 수학과에 입학했고, 그 뒤 프랑스로 건너가 파리 에콜 폴리테크니크에서 응용수학 석사 학위를 받았다.
현재는 에세이와 소설을 집필하면서 연극, 영화 감독으로 활동하고 있다. 그가 두 번째 발표한 영화 '테트리엠 Tetriem'은 1988년 베를린 국제 영화제에서 예술 영화에 주는 인터내셔널 센터 상(CICAE)을 받았다.
현재 그는 그리스 아테네에 거주하고 있다.
001. 감수자의 말...(8)
002. "2보다 큰 모든 짝수는 두 소수의 합으로 나타낼…"...(16)
003. 이졸데는 나의 첫사랑이자 단 한 번뿐인 사랑이었다…...(82)
004. 삼촌은 만족감에서 우러나온 듯한 미소를 짓고 있었다…...(186)
005. 감사의 글...(253)
006. 부록...(254)




